数据预处理
import numpy as np
import matplotlib as plt
import pandas as pd
# 数据读入
dataset = pd.read_csv("winequality-red.csv", sep=";")
# 命名采取下划线的规则
dataset.columns = dataset.columns.str.replace(' ', '_')首先进行导入相关库的操作
将数据以分隔符为;的方式读入。同时由于该文件命名规则不符合python的命名规则,所以我调用了函数将空格替换成了下划线_
效果如下:
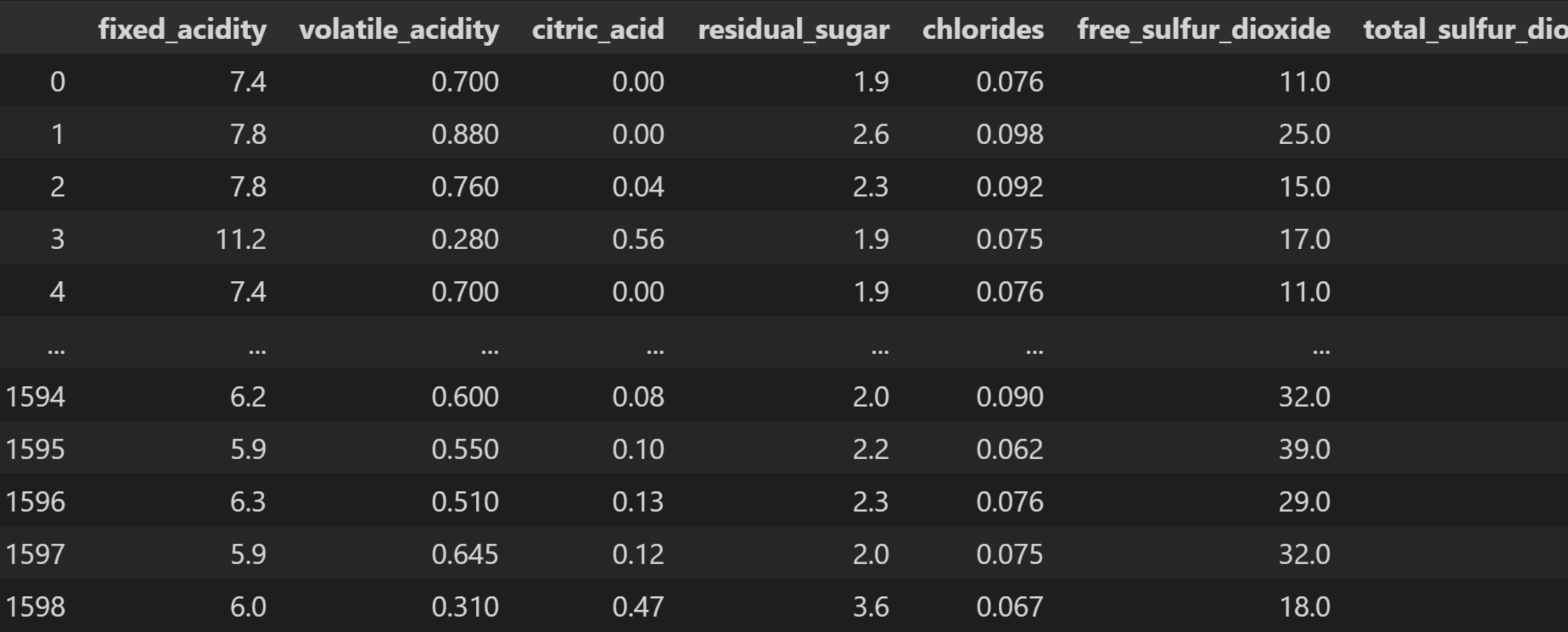
查看数据集的信息
dataset.info()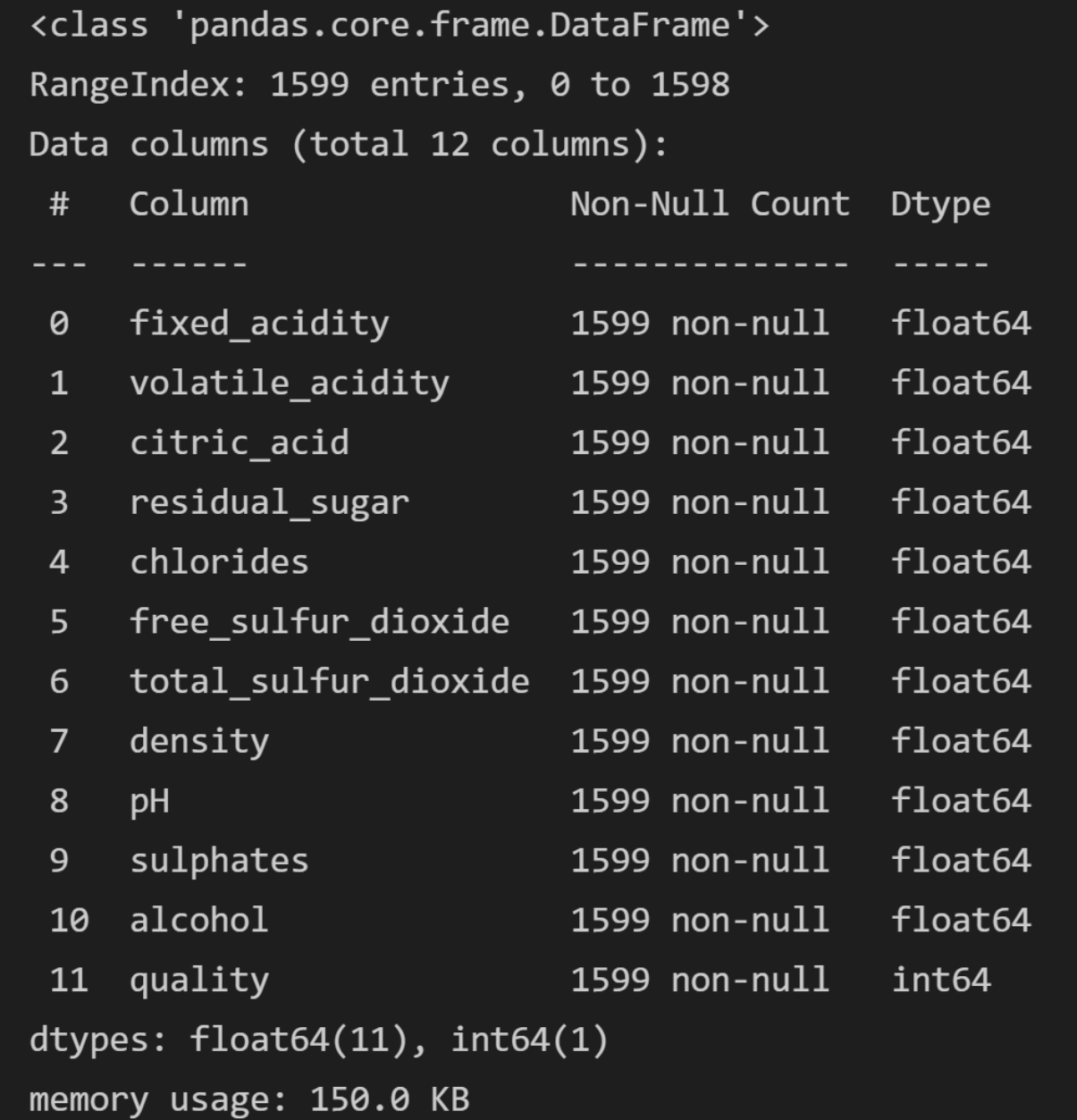
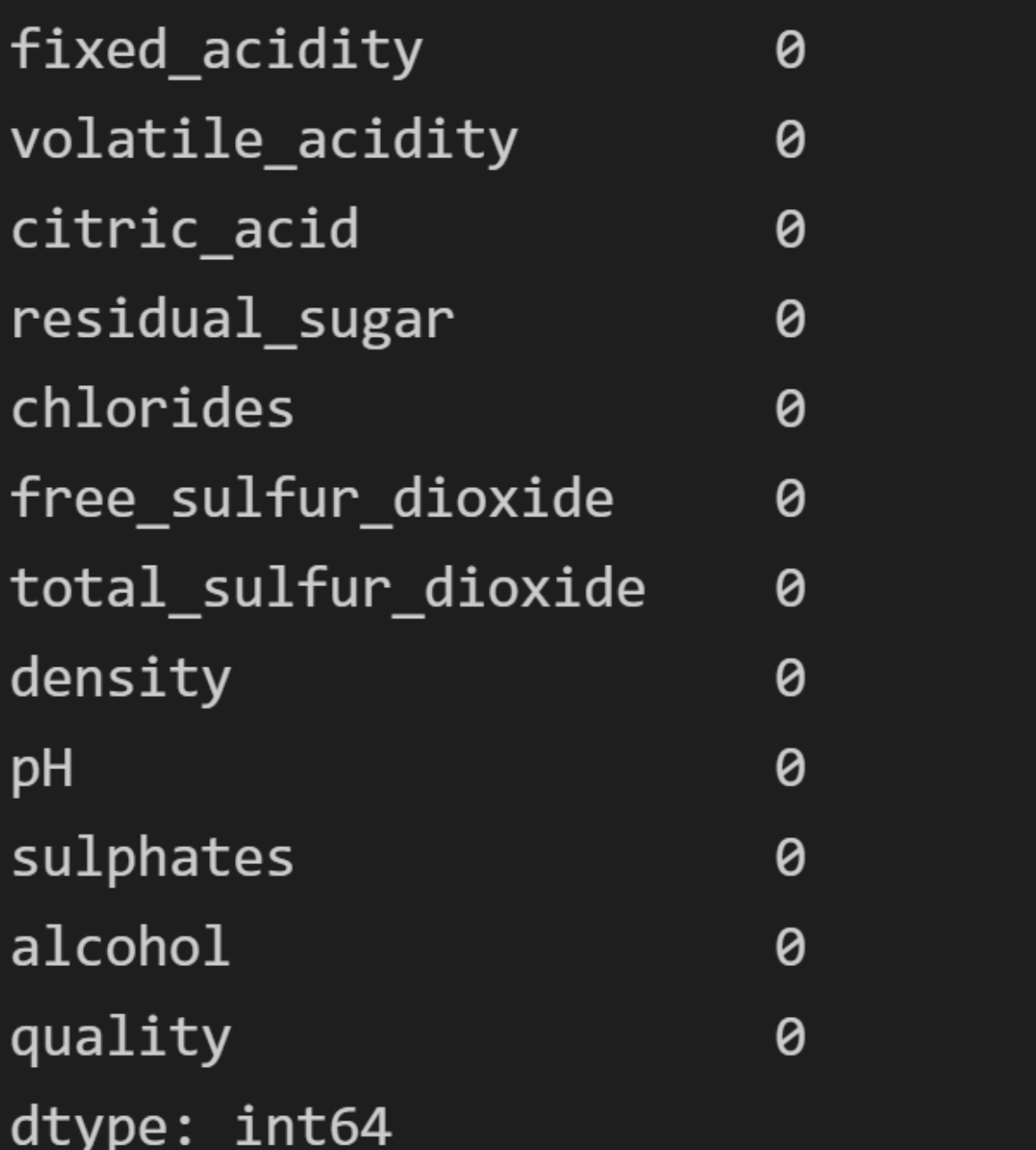
判断是否具有缺失值
# 查看数据是否存在缺失值
dataset.isnull().sum(axis = 0)根据此操作,可以预测是否需要进行缺失值处理,通过数据分析后,效果并没有让我们失望,无一例缺失值!
最终由于Quality 类别太细,等级分为0-10,分布太广,故采取二分类的方式:
将等级分为两个等级,劣质(<=5),优质(>=5)
# 将大于5的设为1,其余设为0
dataset.loc[dataset['quality'] <= 5, 'quality'] = 0
dataset.loc[dataset['quality'] > 5, 'quality'] = 1图像分析
采取直方图的方式进行分析
分析发现各类属性的取值范围差别较大,同时分布也不一致,需要进行归一化处理
dataset.hist(figsize=(10, 10))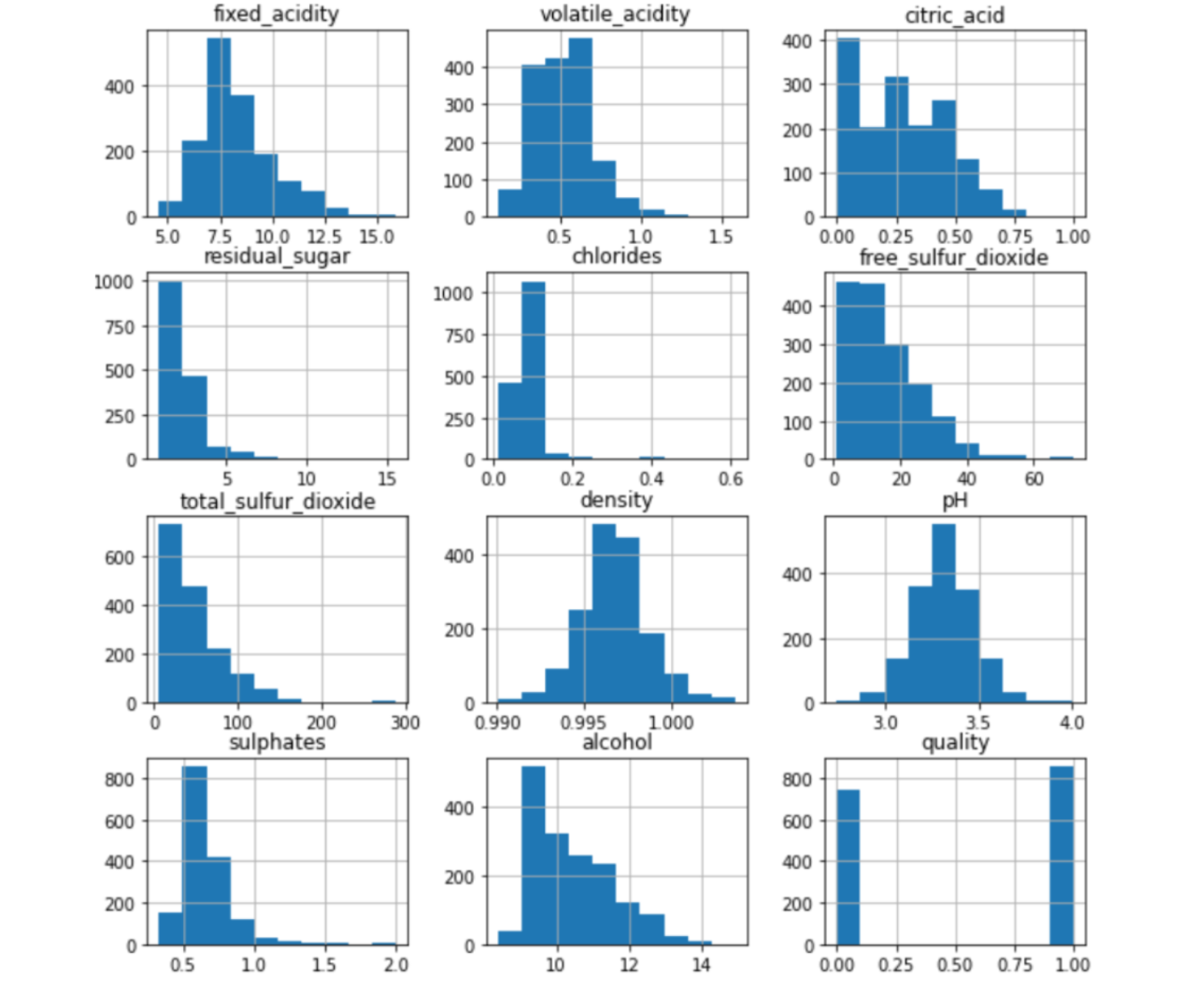
数据归一化
利用公式:$x^*=\frac {x-min}{max-min}$对数据进行归一化处理
# 将数据转成numpy
red = dataset.to_numpy()
# 对数据进行归一化处理
mins = red.min(0) # 返回每一列最小值的列表
maxs = red.max(0) # 返回每一列最大值的列表
ranges = maxs - mins # 最大值列表 - 最小值列表 = 差值列表
norm_red = np.zeros(np.shape(red)) # 用于存储归一化后的数据
row = red.shape[0] # 数据集的行数
norm_red = red - np.tile(mins, (row, 1)) # 矩阵每一列数据都减去每一列的最小值
norm_red = norm_red / np.tile(ranges, (row, 1)) # 最终归一化得到的数据算法的训练与评价
1. 采用神经网络算法
x = norm_red[:, :-1] # 取前面10列
y = norm_red[:, -1: ] # 取最后一列quality
# 使用神经网络算法
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
x_train,x_test,y_train,y_test = train_test_split(x, y, test_size=0.20, random_state=5)
# random_state的设置是为了保证每次结果相同
mlp_model = MLPClassifier(hidden_layer_sizes=(128, 128), max_iter=1000, activation='tanh', random_state=15)
mlp_model.fit(x_train, y_train) # 训练
accuracy = mlp_model.score(x_test, y_test) # 正确率
print('神经网络模型的预测准确率是:', accuracy)算法流程:
首先取出前十列作为x,最后一列quality作为y
然后通过train_test_split函数进行训练集与测试集的划分,random_state的设置是为了保证每次结果相同
通过设置两层隐藏层,大小为128
得到神经网络模型的最终预测准确率为0.784375
2. 采用SVM算法
x = norm_red[:, :-1] # 取前面10列
y = norm_red[:, -1: ] # 取最后一列quality
# 使用SVM算法
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
x_train,x_test,y_train,y_test = train_test_split(x, y, test_size=0.20, random_state=5)
mlp_model = SVC(C=1e4, gamma='auto', kernel='rbf')
mlp_model.fit(x_train, y_train) # 训练
accuracy = mlp_model.score(x_test, y_test) # 正确率
print('SVM的预测准确率是:', accuracy)1. 简介:
SVM(支持向量机)主要用于分类问题,主要的应用场景有字符识别、面部识别、行人检测、文本分类等领域。
通常SVM用于二元分类问题,对于多元分类通常将其分解为多个二元分类问题,再进行分类。
2. 算法流程:
首先取出前十列作为x,最后一列quality作为y
然后通过train_test_split函数进行训练集与测试集的划分,random_state的设置是为了保证每次结果相同
设置迭代回合数为10000,gamma参数为auto
同时设定核函数为高斯核函数,其形式为:$K(x,z)=exp(\frac {-\parallel x-z\parallel^2 }{2\sigma^2} )$
得到SVM模型的最终预测准确率为0.79375
3. 采用KNN算法
x = norm_red[:, :-1] # 取前面10列
y = norm_red[:, -1: ] # 取最后一列quality
# 使用KNN算法
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
x_train,x_test,y_train,y_test = train_test_split(x, y, test_size=0.20, random_state=5)
mlp_model = KNeighborsClassifier(n_neighbors=4)
mlp_model.fit(x_train, y_train) # 训练
accuracy = mlp_model.score(x_test, y_test) # 正确率
print('KNN的预测准确率是:', accuracy)1. 简介:
KNN是一种非参的,惰性的算法模型。什么是非参,什么是惰性呢?
非参的意思并不是说这个算法不需要参数,而是意味着这个模型不会对数据做出任何的假设,与之相对的是线性回归(我们总会假设线性回归是一条直线)。也就是说KNN建立的模型结构是根据数据来决定的,这也比较符合现实的情况,毕竟在现实中的情况往往与理论上的假设是不相符的。
惰性又是什么意思呢?想想看,同样是分类算法,逻辑回归需要先对数据进行大量训练(tranning),最后才会得到一个算法模型。而KNN算法却不需要,它没有明确的训练数据的过程,或者说这个过程很快。
2. 算法流程:
首先取出前十列作为x,最后一列quality作为y
然后通过train_test_split函数进行训练集与测试集的划分,random_state的设置是为了保证每次结果相同
通过不断调参发现设置n的值为4时效果最佳。
得到KNN模型的最终预测准确率为0.75625
4.采用logistic回归方法
x = norm_red[:, :-1] # 取前面10列
y = norm_red[:, -1: ] # 取最后一列quality
# 使用logistic算法
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
x_train,x_test,y_train,y_test = train_test_split(x, y, test_size=0.20, random_state=5)
mlp_model = LogisticRegression(C=1e3, solver='liblinear', multi_class='auto')
mlp_model.fit(x_train, y_train) # 训练
accuracy = mlp_model.score(x_test, y_test) # 正确率
print('逻辑回归的预测准确率是:', accuracy)得到logistic模型的最终预测准确率为0.78125
综上所述,四种模型的预测准确率如下:
神经网络模型:0.784375
SVM模型:0.79375
KNN模型:0.75625
logistic模型:0.78125
发现在这个问题中,SVM算法训练出来的模型效果最佳



